1) 45

2) 2Kg

3) 4

4) peso Asino = 140 e peso Mulo = 100

5) 18 Conigli e 14 Oche

6) Nella pesata ci metto una moneta presa dal primo sacchetto, due dal secondo e cosi' via fino a dieci monete dal decimo sacchetto. Se tutte fossero da 1 gr il risultato sarebbe 55 gr. Invece la presenza delle monete piu' leggere fara' calare il peso di 0.9 gr per ogni moneta leggera.
Chiamando X il peso ottenuto avro': (55 - X) / 0.9 = numero di monete leggere presenti sul piatto e quindi indice del sacchetto che le contiene.

7) A e B attraversano il ponte e B torna indietro (4 min)
C e D attraversano il ponte e A torna indietro (15 min)
A e B attraversano il ponte e sono tutti in salvo (17 min).

8) Un tetraedro

9) Divido in 3 gruppi di 9 palline. Metto un gruppo sul piatto e uno sull'altro. Se sono dello stesso peso, la pallina di piombo si trova nel terzo gruppo, se uno dei piatti scende, allora la pallina di piombo si trova in quel gruppo.
Con questo procedimento con una pesata individuo due terzi delle palline che sicuramente sono di ferro e devo continuare la ricerca solo sul terzo rimanente.
Quindi con tre pesate scopro la pallina di piombo nascosta in 3 alla 3 palline.

10) 31 uomini e 22 donne

11) Spostando 2 fiammiferi si ottiene:

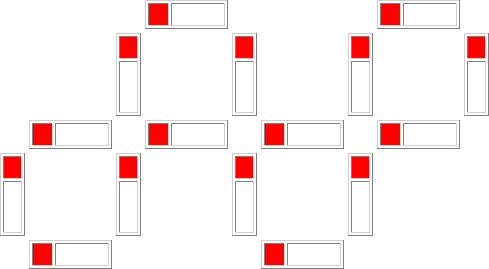
12)

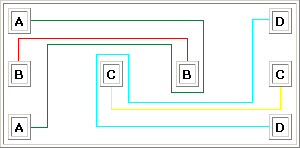
13) Una lampadina può essere: accesa, spenta, calda, fredda.
La procedura è la seguente.

• Il primo interruttore non lo tocco.

• Il secondo lo attivo per 10 minuti e poi lo disattivo.

• Il terzo lo attivo.

Dopo aver compiuto queste operazioni entro immediatamente nella stanza, osservo e tocco la lampadina.

• Se è accesa, l'interruttore cercato è il terzo.

• Se è spenta e calda, l'interruttore è il secondo.

• Se è spenta e fredda, l'interruttore è il primo.

14) Trasformo VII in "radice quadrata di I" spostando un bastoncino.

15) Il numero è 42857
Premetto 1: 142.857 * 3 = 428.571
Aggiungo 1 : 428.571

16) Le terne di numeri il cui prodotto e` 36 (con le somme vicino) sono: 36-1-1 (38); 18-2-1 (21); 12-3-1 (16); 9-4-1 (14); 9-2-2 (13); 6-6-1 (13); 6-3-2 (11); 4-3-3 (10).
Il secondo matematico sa qual e` la somma (vede il numero della casa) ma non sa rispondere. Questo significa che la somma e` 13, l'unico numero che appare due volte. La seconda affermazione del primo matematico ci dice che la risposta giusta e` 9-2-2.

17) Il trucco qui e` il fatto che il presentatore non apre una porta a caso, ma ne sceglie una con una capra. Supponiamo di avere scelto la prima porta: in questo momento abbiamo probabilita` 1/3 che l'auto sia dietro una qualunque porta. Nei due casi in cui l'auto sia nella porta 2 o 3, il presentatore apre rispettivamente la porta 3 o 2, e se noi cambiamo scelta vinciamo (probabilita` 2/3); se avevao scelto la porta giusta, lui ne apre a caso una delle altre (probabilita` 1/6 per ciascuna) e se noi cambiamo perdiamo (probabilita` 1/3). Quindi ci conviene cambiare porta

18) La risposta tipica e` "sette", perche` la parola "quattro" ha sette lettere. Come gia` scritto, le risposte possibili sono infinite...

19) Una piccola città, in qualche sperduto luogo della terra, è infestata dai lupi mannari, cioè ci sono alcune persone che durante le notti di luna piena si trasformano in lupi feroci. Si può quindi ragionevolmente pensare che almeno uno degli abitanti di questo strano luogo sia un lupo mannaro. Per fare fronte a questa situazione il sindaco della cittadina emette un'ordinanza, la quale prevede che ogni cittadino che sappia di essere un lupo mannaro, si debba uccidere appena lo scopre. Dato che gli abitanti del luogo sono tutti dei cittadini rispettosi delle leggi, si può dare per certo che effettivamente ogni abitante che scopra di essere un lupo mannaro si uccida. Purtroppo però, un lupo mannaro non si accorge di esserlo e quindi lo può solo capire dall'ossevazione di quello che gli sta intorno. A questo punto occorre ricordare che tutte le notti, e quindi in particolare quelle di plenilunio, ogni cittadino incontra tutti gli altri, e pertanto è in grado di vedere i lupi mannari anche se non può comunicare con loro. Dopo la terza notte di luna piena vengono ritrovati i cadaveri di alcuni lupi mannari. Voi dovete scoprire quanti sono i lupi ritrovati e soprattutto perchè sono stati ritrovati soltanto dopo la terza notte, mentre nelle due precedenti non si è avuto alcun ritrovamento.

20) Ecco la soluzione di questo semplice gioco.

21) Certo, visto che il filo rimarra` sollevato di 100/(2 pi) ~= 16 cm e i gatti sono piuttosto flessuosi.

22) Il problema si risolve se N ed M sono primi tra loro, e la soluzione (non necessariamente la piu` breve) ricorda gli algoritmi di divisibilita`. Supponiamo per comodita` M < N per sapere qual e` il recipiente piu` piccolo. Versiamo acqua dal recipiente grande al piccolo fino a riempirlo, e a questo punto travasiamo l'acqua nel recipiente medio. Se a un certo punto esso ha N litri, siamo a posto; altrimenti prima o poi si riempie. Allora versiamo l'acqua dal medio al grande, e finiamo di travasare dal piccolo al medio. La situazione e` simile a quella iniziale, modulo una classe di resto (il numero di litri d'acqua nel recipiente medio). Ripetendo le operazioni da capo, scorreremo tutte le classi di resto, e quindi avremo anche a un certopunto il valore N cercato.

23) Il numero minimo di noci di cocco possibile e` 15621. Per arrivare a questo risultato, si noti innanzitutto che si puo` sommare a piacere multipli di 5^6=15625 alla soluzione: infatti un mucchio di dimensione 15625 e` il piu` piccolo per cui si possano fare esattamente le sei divisioni con rimozione di un quinto ogni volta. L'idea risolutiva consiste nel trovare un numero *negativo* piccolo soluzione dell'equazione (anche se non del problema, ovviamente), e sommarci 15625. La "soluzione" cercata e` -4. Infatti se io ho 4 "noci negative", posso fare cinque gruppi di "una noce negativa" e dare una noce (reale!) alla scimmia. A questo punto, il mucchio di noci ne ha di nuovo "quattro negative", e quindi si puo` andare avanti a piacere.
Sommando 15625 a -4, otteniamo appunto 15621

24) Il barbone aveva raccolto 22 mozziconi con i quali ha confezionato 5 sigarette con l'avanzo di due mozziconi. Coi 7 mozziconi rimasti dopo aver fumato le prime 5, ha fabbricato un'altra sigaretta con l'avanzo di 3 mozziconi. Dopo averla fumata rimane con 4 mozziconi coi quali costruisce la settima sigaretta. Alla fine quindi gli rimane 1 mozzicone.